

|
|
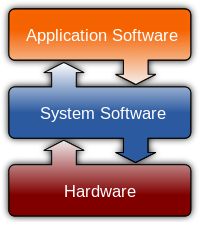
|
help2002This forum is provided to promote discussion amongst students enrolled in CITS2002 .Please consider offering answers and suggestions to help other students! And if you fix a problem by following a suggestion here, it would be great if other interested students could see a short "Great, fixed it!" followup message. |